The NESA Maths Reference Sheet is an outstanding helpful useful resource… in the event you know how to utilize it! Navigate options (along with trigonometric ones!) and relations with our Closing NESA Maths Reference Sheet Data.
Whereas memorisation has its place in finding out, Matrix recommends that faculty college students be taught to derive their responses and study to use these formulae appropriately. As a bonus, we’ve included a nifty HSC Maths Cheatsheet so as to receive and print out!
Click on on on the following formulation to see what they indicate and apply them to a apply question!
| Capabilities |
| (x=frac{-b± sqrt{b^2-4ac}}{2a})
(textual content material{For} ax^3 + bx^2 +cx + d = 0 |
| Relations |
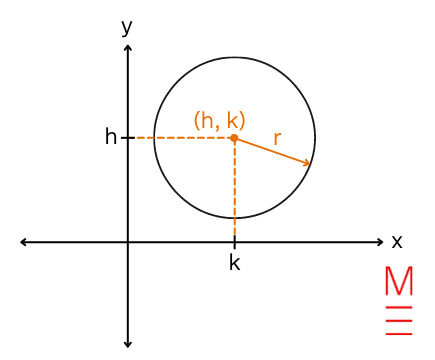
| ((x-h)^2+(y-k)^2=r^2) |
| Logarithmic and Exponential Capabilities |
| (textual content material{log}_a a^x = x = a^{textual content material{log}_a x})
(textual content material{log}_a x = frac{textual content material{log}_b x}{textual content material{log}_b a}) (a^x = e^{xtext{In}a}) |
| Trigonometric Capabilities |
| ( textual content material{sin}A = frac{textual content material{opp}}{textual content material{hyp}}, textual content material{cos}A = frac{textual content material{adj}}{textual content material{hyp}}, textual content material{tan}A = frac{textual content material{opp}}{textual content material{adj}})
(A= frac{1}{2}abtext{ sin}C) (frac{a}{textual content material{sin}A} = frac{b}{textual content material{sin}B} = frac{c}{textual content material{sin}C}) (c^2=a^2+b^2-2abtext{ cos}C) (textual content material{cos}C = frac{a^2+b^2-c^2}{2ab}) (l=r theta) (A=frac{1}{2}r^2theta)
Trigonometric identities (textual content material{sec}A = frac{1}{textual content material{cos}A}, textual content material{cos}A ≠0) (textual content material{cosec}A = frac{1}{textual content material{sin}A}, textual content material{sin}A ≠0) (textual content material{cot}A = frac{textual content material{cos}A}{textual content material{sin}A}, textual content material{sin}A ≠0) (textual content material{cos}^2x+textual content material{sin}^2x=1)
Compound angles (textual content material{sin}(A+B)=textual content material{sin}Atext{cos}B+textual content material{cos}Atext{sin}B) (textual content material{cos}(A+B)=textual content material{cos}Atext{cos}B-text{sin}Atext{sin}B) (textual content material{tan}(A+B)=frac{textual content material{tan}A+textual content material{tan}B}{1-text{tan}Atext{tan}B}) (textual content material{If } t=textual content material{tan} frac{A}{2} textual content material{ then } ) (textual content material{cos}Atext{cos}B=frac{1}{2}[text{cos}(A-B)+text{cos}(A+B)]) (textual content material{sin}Atext{sin}B=frac{1}{2} [text{cos}(A-B) -text{cos}(A+B)]) (textual content material{sin}Atext{cos}B = frac{1}{2} [text{sin}(A+B)+text{sin}(A-B)]) (textual content material{cos}Atext{sin}B=frac{1}{2}[text{sin}(A+B)-text{sin}(A-B)]) (textual content material{sin}^2nx=frac{1}{2}(1-text{cos}2nx)) (textual content material{cos}^2nx=frac{1}{2}(1+textual content material{cos}2nx)) |
Capabilities
| Use | Formulation | Variables |
| Clear up quadratic equations | (x=frac{-b± sqrt{b^2-4ac}}{2a}) | a, b and c are the coefficients of a quadratic equation throughout the sort:(ax^2+bx+c=0) |
Once more to prime
Subsequent half: Relations
Occasion 12:
Ponder the following equation: (-2y^2+3y+1=0)
Uncover all the choices of (y).
Decision 12:
| Though the above equation makes use of (y) as a variable instead of (x), the quadratic system works the similar strategy.
begin{align*} Subsequently, substitute (a=-2), (b=3) and (c=1) into (y=frac{-b± sqrt{b^2-4ac}}{2a}): begin{align*} |
Once more to prime
| Use | Formulation | Variables |
| Cubic roots | begin{align*} textual content material{For} ax^3 + bx^2 +cx + d &= 0: α+β+γ &= – frac{b}{a} αβ+αγ+βγ &= frac{c}{a} textual content material{and } αβγ &= -frac{d}{a} end{align*} |
α, β and γ are roots of a cubic equation throughout the sort: (ax^3 + bx^2 +cx + d = 0) |
Once more to prime
Occasion 13:
(x=1) and (x=3) are two choices to the monic equation: (ax^3 + bx^2 +cx + d = 0)
Given that the product of the roots is -6, uncover the coefficients (a,b,c) of this cubic polynomial.
Decision 13:
| The question states that the equation is monic. Which implies, a=1.
begin{align*} αβγ &= -frac{d}{a} α+β+γ &= – frac{b}{a} αβ+αγ+βγ &= frac{c}{a} It’s provided that (x=1) and (x=3) are choices to the cubic equation, (x=1) and (x=3) are two roots of the equation. Subsequently, substitute (α=1) and (β=3) into (αβγ = -6): begin{align*} To go looking out the coefficients b and c (we’ve already found (a=1) and (d=6)): Substitute (α=1), (β=3) and (γ=-2) into equation 1: (α+β+γ = -b) and equation 2: (αβ+αγ+βγ = c): begin{align*} textual content material{Equation 2: } (1)(3)+(1)(-2)+(3)(2) &= c Resulting from this reality, the coefficients of the equation (ax^3 + bx^2 +cx + d = 0) are (a=1), (b=-2),(c=7) and (d=6). |
Once more to prime
Relations
| Use | Formulation | Rationalization |
| Cartesian equation of a circle | ((x-h)^2+(y-k)^2=r^2) | Cartesian equation of a circle centred at (h, okay) with radius = r
|
Once more to prime
Subsequent half: Logarithmic and Exponential Capabilities
Occasion 14:
The centre of a circle lies on the intersection of two traces: (y = x) and (y = 2x – 4)
Given that the realm of this circle is (16π ) gadgets2, uncover the Cartesian equation of this circle.
Decision 14:
| To go looking out the centre of the circle, first we concurrently clear up the equations (y = x) and (y = 2x – 4) to hunt out their stage of intersection.
begin{align*} textual content material{Substitute } x &= 4 textual content material{ into } y = 2x – 4 : ⇒ textual content material{Centre of circle (h, okay) } & = (4, 4) To go looking out the radius r of the circle, we’re in a position to make use of the information that the realm of this circle is (16π ) gadgets2. The system for the realm of a circle is: ( A = pi r^2 ) begin{align*} The equation of the circle is: ((x-h)^2+(y-k)^2=r^2) the place ((h, okay)) = ((4, 4)) and (r = 4) begin{align*} |
Once more to prime
Logarithmic and Exponential Capabilities
| Formulation | Software program |
| (textual content material{log}_a a^x = x = a^{textual content material{log}_a x}) | Simplifying and manipulating expressions. |
| (textual content material{log}_a x = frac{textual content material{log}_b x}{textual content material{log}_b a}) | Most calculators can calculate (textual content material{log}_{10}) and (textual content material{ln}). To enter logarithms with out base 10 or e, you have to use this technique convert your logarithm into an expression involving logarithms with solely base 10 or e.
e.g. (textual content material{log}_8 9 = frac{textual content material{log}_{10} 9}{textual content material{log}_{10} 8} = frac{ textual content material{ln}9}{textual content material{ln}8}) (textual content material{log}_2 5 = frac{textual content material{log}_{10} 5}{textual content material{log}_{10} 2}= frac{ textual content material{ln}5}{textual content material{ln}2}) |
| (a^x = e^{xtext{ln}a}) | To mix expressions throughout the sort (a^x):
begin{align*} Analysis your data of integration by substitution proper right here. |
Once more to prime
Trigonometric Capabilities
| Use | Formulation | Rationalization |
| Trigonometric options | begin{align*} textual content material{sin}A = frac{textual content material{opp}}{textual content material{hyp}} textual content material{cos}A = frac{textual content material{adj}}{textual content material{hyp}} textual content material{tan}A = frac{textual content material{opp}}{textual content material{adj}} end{align*} |
Once more to prime
Occasion 15:
Given the beneath right-angle triangle, uncover the price of the following trigonometric expressions:
a) sinA
b) cos(90°-A)
c) tan90°
Decision 15:
| a) sinA = (frac{4}{5})
b) cos(90°-A) = sinA = (frac{4}{5}) Alternatively, recognise that (90°-A) is an angle throughout the triangle. Subsequently, cos(90°-A) = (frac{textual content material{adj}}{textual content material{hyp}}) = (frac{4}{5}) c) tan90° = undefined As we’re capable of see on this correct angle triangle, the scale reverse 90° is the hypotenuse. Subsequently, the expression ( textual content material{tan}90° = frac{textual content material{opp}}{textual content material{adj}}) is undefined. |
Once more to prime
| Use | Formulation | Rationalization |
| Area of a triangle | (A= frac{1}{2}abtext{sin}C) | |
Once more to prime
Occasion 16:
Given that the following triangle has an house of (4 sqrt{3}) cm2, uncover the scale x.
Decision 16:
| Substitute (A= 4 sqrt{3}), (a=3), (b=x) and (C=60°) into (A= frac{1}{2}abtext{sin}C):
begin{align*} |
Once more to prime
| Use | Formulation | Rationalization |
| Sine rule | (frac{a}{textual content material{sin}A} = frac{b}{textual content material{sin}B} = frac{c}{textual content material{sin}C}) | |
| Cosine rule | (c^2=a^2+b^2-2abtext{cos}C)
This equation will even be rearranged as: (textual content material{cos}C = frac{a^2+b^2-c^2}{2ab}) |
Once more to prime
Occasion 17:
Uncover dimension x. Giver your reply to the closest 3 decimal places.
The diagram is simply not to-scale.
Decision 17:
| With a goal to make use of the sine rule to hunt out x, we have now to know the angle θ that’s reverse dimension x.
begin{align*} Thus, we’re in a position to make use of the sine rule: Substitute (a=4), (A=30°), (b=x), (B=θ=105°) into (frac{a}{textual content material{sin}A} = frac{b}{textual content material{sin}B}): begin{align*} |
Once more to prime
| Use | Formulation | Rationalization |
| Arc dimension of a sector
(using θ in radians: ( pi ^c = 180°)) |
(l=r theta) | begin{align*} l&= textual content material{arc dimension} theta &= textual content material{angle of sector in radians} r &= textual content material{radius} end{align*} |
| Area of a sector
(using θ in radians: ( pi ^c = 180°)) |
(A= frac{1}{2} r^2 theta) |
Once more to prime
Occasion 18:
a) Sal is fencing a paddock for his sheep. He wishes to make the paddock the type of a sector with a radius of 6 metres. If he has (12 + 2π) metres of fencing, what’s the angle of an important sector he can completely enclose? Give your reply as a exact value in radians.
b) Subsequently, uncover the utmost house of Sal’s paddock.
Decision 18 a):
| The subsequent diagram illustrates the paddock. 12 + 2π &= 6 + 6 + l l &= 2π end{align*}Subsequently, the arc dimension of an important sector Sal can enclose is (2π). Nonetheless, this isn’t our final reply as we’re required to hunt out the angle of an important sector. Substitute (l = 2π) and (r=6) into (l=r theta):begin{align*} 2π &= 6 events theta theta &= frac{π}{3} ∴ textual content material{Angle of an important sector} &= frac{π}{3}^c end{align*} |
Decision 18 b):
| We’re provided that the radius of the sector is 6 metres and partly a), we found that an important doable angle of the sector is (frac{π}{3}^c).
So, to hunt out an important house of the sector, substitute (r=6) and (theta=frac{π}{3}^c) into (A= frac{1}{2} r^2 theta): begin{align*} |
Once more to prime
Trigonometric identities
| Identification | Variables |
| (textual content material{sec}A = frac{1}{textual content material{cos}A}, textual content material{cos}A ≠0) | Angle (A) can take any variable (except for the place exceptions are significantly well-known) and the identification will keep true. |
| (textual content material{cosec}A = frac{1}{textual content material{sin}A}, textual content material{sin}A ≠0) | |
| (textual content material{cot}A = frac{textual content material{cos}A}{textual content material{sin}A}, textual content material{sin}A ≠0) | |
| (textual content material{cos}^2x+textual content material{sin}^2x=1) |
Once more to prime
Occasion 19:
Present that: (textual content material{tan}θtext{sin}θ + textual content material{cos}θ = textual content material{sec}θ)
Decision 19:
| begin{align*} LHS &= textual content material{tan} theta textual content material{sin} theta + textual content material{cos} theta textual content material{Since } textual content material{tan} theta = frac{ textual content material{sin} theta }{ textual content material{cos} theta }, LHS &= frac{ textual content material{sin} theta }{ textual content material{cos} theta } events textual content material{sin} theta + textual content material{cos} theta &= frac{ textual content material{sin}^2 theta }{ textual content material{cos} theta } + frac{ textual content material{cos}^2 theta }{ textual content material{cos} theta } &= frac{ textual content material{sin}^2 theta + textual content material{cos}^2 theta }{ textual content material{cos} theta } textual content material{Since } textual content material{sin}^2 theta + textual content material{cos}^2 theta=1, &= frac{1}{ textual content material{cos} theta } &= textual content material{sec} theta &= RHS ∴ textual content material{tan} theta textual content material{sin} theta + textual content material{cos} theta = textual content material{sec} theta end{align*} |
Once more to prime
Compound angles
Rising a sum of angles in a trigonometry function
| Identification | Variables |
| (textual content material{sin}(A+B)=textual content material{sin}Atext{cos}B+textual content material{cos}Atext{sin}B) | (A, B ∈ R)
Angle (A) and (B) can take any value (they’re typically equal or unequal) and the identification will keep true. |
| (textual content material{cos}(A+B)=textual content material{cos}Atext{cos}B-text{sin}Atext{sin}B) | |
| (textual content material{tan}(A+B)=frac{textual content material{tan}A+textual content material{tan}B}{1-text{tan}Atext{tan}B}) |
Once more to prime
Occasion 20:
Uncover the exact value of (cos75º).
Decision 20:
| begin{align*} textual content material{cos}75º &= textual content material{cos}(45+30)º textual content material{Since } textual content material{cos}(A+B)=textual content material{cos}Atext{cos}B-text{sin}Atext{sin}B textual content material{cos}(45+30)º &= textual content material{cos}45text{cos}30-text{sin}45text{sin}30 &= frac{ sqrt{2}}{2} events frac{ sqrt{3}}{2} – frac{ sqrt{2}}{2} events frac{1}{2} &= frac{ sqrt{6}}{4} – frac{ sqrt{2}}{4} ∴ textual content material{cos}75º &= frac{ sqrt{6} – sqrt{2}}{2} end{align*} |
Once more to prime
T-formula
| Formulation | Rationalization |
| begin{align*} textual content material{If } t=textual content material{tan} frac{A}{2} textual content material{ then } textual content material{sin}A &= frac{2t}{1+t^2} textual content material{cos}A &= frac{1-t^2}{1+t^2} textual content material{tan}A &= frac{2t}{1-t^2} end{align*} |
(A ∈ R)
Substitute sinA, cosA or tanA with these ‘t-values’. That strategy you gained’t ought to address trigonometric options, solely algebraic expressions involving t. Upon getting simplified your expression involving t, usually you’ll have to substitute (t=textual content material{tan} frac{A}{2}) to hunt out the values of (A). Phrase: When A = 180°, (t=textual content material{tan} frac{A}{2} = textual content material{tan}90) is undefined. Which means that you just’ll wish to individually confirm whether or not or not A = 180° it’s a decision in the event you use the t-formula. See Occasion 21 beneath. |
Once more to prime
Occasion 21:
Given (2text{cos}2B – textual content material{sin}2B = 1), clear up for (B), (0 le B le 180°):
If very important, give your options to the closest 2 decimal places.
Decision 21:
| begin{align*} textual content material{Let } t &= textual content material{tan}B ⇒ textual content material{sin}2B &= frac{2t}{1+t^2} textual content material{cos}2B &= frac{1-t^2}{1+t^2} textual content material{tan}2B &= frac{2t}{1-t^2} textual content material{Given that }2text{cos}2B – textual content material{sinB}2B &= 1 |
Once more to prime
Manipulating a product of trigonometric options proper right into a sum of trigonometric options
| Identification | Variables |
| (textual content material{cos}Atext{cos}B=frac{1}{2}[text{cos}(A-B)+text{cos}(A+B)]) | Angle (A) and (B) can take any variable (they’re typically equal or unequal) and the identification will keep true. |
| (textual content material{sin}Atext{sin}B=frac{1}{2} [text{cos}(A-B) -text{cos}(A+B)]) | |
| (textual content material{sin}Atext{cos}B = frac{1}{2} [text{sin}(A+B)+text{sin}(A-B)]) | |
| (textual content material{cos}Atext{sin}B=frac{1}{2}[text{sin}(A+B)-text{sin}(A-B)]) |
Once more to prime
Occasion 22:
Uncover the exact value of the product of (textual content material{cos}15º) and (textual content material{sin}45º).
Decision 22:
| begin{align*} textual content material{Since } textual content material{cos}Atext{sin}B & =frac{1}{2}[text{sin}(A+B)-text{sin}(A-B)] ⇒ textual content material{cos}15ºtext{sin}45º &= frac{1}{2}[text{sin}(15+45)-text{sin}(15-45)] &= frac{1}{2}[text{sin}(60)-text{sin}(-30)] &= frac{1}{2}[frac{ sqrt{3}}{2}+ frac{1}{2} ] ∴textual content material{cos}15ºtext{sin}45º &= frac{sqrt{3}+1}{4} end{align*} |
Once more to prime
Double angle identities
| Identification | Variables |
| (textual content material{sin}^2nx=frac{1}{2}(1-text{cos}2nx)) | (x, n ∈ R) |
| (textual content material{cos}^2nx=frac{1}{2}(1+textual content material{cos}2nx)) |
Once more to prime
Occasion 23:
Think about (2(textual content material{sin}22.5º)^2). Give your reply in exact sort.
Decision 23:
| begin{align*} textual content material{Since } textual content material{sin}^2nx &=frac{1}{2}(1-text{cos}2nx) ⇒ 2(textual content material{sin}22.5º)^2 &= 2 events frac{1}{2}(1-text{cos}45º) &= 1- frac{ sqrt{2}}{2} &= frac{ 2- sqrt{2}}{2} ∴2(textual content material{sin}22.5º)^2 &= frac{ 2- sqrt{2}}{2} end{align*} |
Once more to prime
,